5 facts about scaling

Scaling is an important – but often misunderstood – component of your ATAR calculation. Here are five facts to help you understand why, what and how we scale.

1. Scaling is done for a specific purpose: it's the first step in the calculation of the ATAR.
2. The underlying principle of scaling is that you should be neither advantaged nor disadvantaged by choosing one combination of HSC courses over another.
3. Scaling reflects the strength of the competition in a course, not the perceived difficulty of the course.
4. Scaling is based on a rigorous and unbiased mathematical model.
5. Scaling does not change the ranking of students within a course.

Fact 1: Scaling is done for a specific purpose: it's the first step in the calculation of the ATAR.

In turn, the ATAR has a very specific purpose: it is one tool used by universities when selecting applicants for admission.

The ATAR is a rank, not a mark out of 100. It is based on your achievement in all your HSC courses and tells you where you are positioned compared to other students in NSW. Think of it like a running race: your HSC is your time (and is not compared to anyone else's time), and your ATAR is your place (first, second, third, and so on). Your position in the race depends not only on your time but on the times of the students you are competing with.

For universities, a student’s rank in the HSC is a valid predictor of their success in tertiary studies.

Fact 2: The underlying principle of scaling is that you should be neither advantaged nor disadvantaged by choosing one combination of HSC courses over another.

If everyone studied the same HSC courses, scaling wouldn’t be necessary. We could easily compare and rank students.

But each year in NSW, around 55,000 ATAR-eligible HSC students study roughly 27,000 different combinations of HSC courses. And close to 20,000 of these students are the only ones studying their particular combination. So how can we make fair comparisons and rank students? We need to create a level playing field.

Enter the scaling algorithm: it estimates what your marks would have been if all courses had been studied by all students and all courses had the same mark distribution.

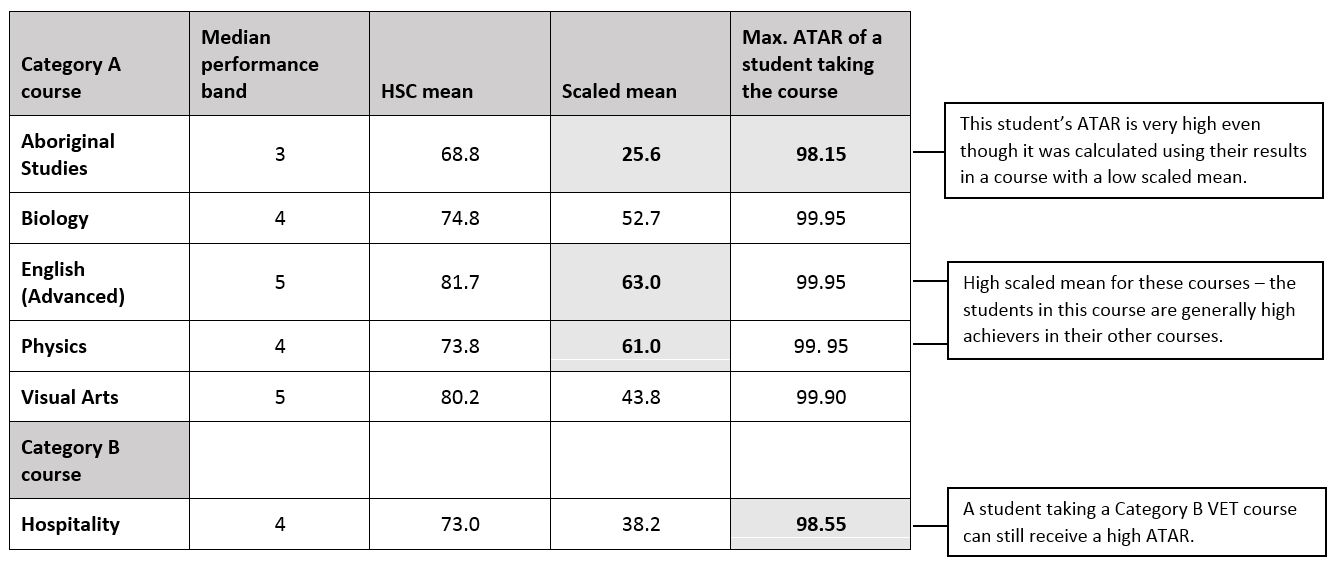
Fact 3: Scaling reflects the strength of the competition in a course, not the perceived difficulty of the course:

• If a course has a high scaled mean it tells us that, on average, the ability of the students in that course is high – in general, they did well in their other courses.
• If a course has a low scaled mean it tells us that the ability of the students in that course ranges from high to low. (It doesn’t mean that you can’t get a high ATAR if you study that course.)

The following table illustrates these points using data from selected 2017 HSC courses.

Fact 4: Scaling is based on a rigorous and unbiased mathematical model.

It requires a lot of detail to explain in full but, in a nutshell, here’s what takes place each year:

• First, raw HSC marks for each course (which are not reported to students) are compared and standardised to a common mean (average mark) and standard deviation (spread of marks).
• Then, the scaled mean and standard deviation for each course is calculated.
• Finally, individual raw marks are scaled.

Now that we have a level playing field, we can rank students. Your ATAR is based on the aggregate of your scaled marks in 10 units of ATAR courses, of which at least 2 must be from English.

Fact 5: Scaling does not change the ranking of students within a course.

If you are ranked towards the top of the state in all your courses, you are more likely to receive a high ATAR. Likewise, if your performance is below average, it makes sense that you will receive a below-average ATAR.

Want to delve deeper?

Take a look at the following publications:

• Report on the Scaling of the 2017 NSW Higher School Certificate
• Calculating the Australian Tertiary Admission Rank in New South Wales – A Technical Report

A preliminary report on the scaling of the 2018 HSC will be published on the UAC website when ATARs are released on Friday 14 December.